Raindrop Elevation & Colour
£0.00
This is one of a set of almost 40 diagrams exploring Rainbows.
Each diagram appears on a separate page and is supported by a full explanation.
- Follow the links embedded in the text for definitions of all the key terms.
- For quick reference don’t miss the summaries of key terms further down each page.
Description
Raindrop Elevation & Colour
TRY SOME QUICK QUESTIONS AND ANSWERS TO GET STARTED
About the diagram
About the diagram
- This diagram deals with how a single raindrop can contribute to the formation of a primary rainbow.
- The diagram shows that a single falling raindrop appears red then orange, yellow, green, blue and finally violet as it falls towards the ground.
- It is the elevation of a droplet relative to the rainbow axis and observer that determines its colour at any moment as it falls.
- Notice that the diagram shows a ray of white light entering the top half of the raindrop and reflecting once off the interior surface before exiting towards the observer. This is always the case if a raindrop is part of a primary bow.
- So this is the sequence:
- At its largest angular distance from the axis, a raindrop appears red to an observer as it enters into the outer edge of the primary bow.
- Moments later, as that same raindrop falls, and its angular distance decreases, it changes colour, first from red and finally to violet. The diagram shows the moments at which it appears red, yellow and blue.
- As it falls further and its angular distance reduces below 40.70 it exits the inside edge of the bow.
- The droplet is now almost invisible but continues to contribute a little to a scattering of white light that fills this area within the arcs with a light glow.
Overview of raindrops
Some key terms
A human observer is a person who engages in observation by watching things.
- In the presence of visible light, an observer perceives colour because the retina at the back of the human eye is sensitive to wavelengths of light that fall within the visible part of the electromagnetic spectrum.
- The visual experience of colour is associated with words such as red, blue, yellow, etc.
- The retina’s response to visible light can be described in terms of wavelength, frequency and brightness.
- Other properties of the world around us must be inferred from light patterns.
- An observation can take many forms such as:
- Watching an ocean sunset or the sky at night.
- Studying a baby’s face.
- Exploring something that can’t be seen by collecting data from an instrument or machine.
- Experimenting in a laboratory setting.
Refraction refers to the way that electromagnetic radiation (light) changes speed and direction as it travels across the boundary between one transparent medium and another.
- Light bends towards the normal and slows down when it moves from a fast medium (like air) to a slower medium (like water).
- Light bends away from the normal and speeds up when it moves from a slow medium (like diamond) to a faster medium (like glass).
- These phenomena are governed by Snell’s law, which describes the relationship between the angles of incidence and refraction.
- The refractive index (index of refraction) of a medium indicates how much the speed and direction of light are altered when travelling in or out of a medium.
- It is calculated by dividing the speed of light in a vacuum by the speed of light in the material.
- Snell’s law relates the angles of incidence and refraction to the refractive indices of the two media involved.
- Snell’s law states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is equal to the ratio of the refractive indices.
In the field of optics, dispersion is shorthand for chromatic dispersion which refers to the way that light, under certain conditions, separates into its component wavelengths, enabling the colours corresponding with each wavelength to become visible to a human observer.
- Chromatic dispersion refers to the dispersion of light according to its wavelength or colour.
- Chromatic dispersion is the result of the relationship between wavelength and refractive index.
- When light travels from one medium (such as air) to another (such as glass or water) each wavelength is refracted differently, causing the separation of white light into its constituent colours.
- When light undergoes refraction each wavelength changes direction by a different amount. In the case of white light, the separate wavelengths fan out into distinct bands of colour with red on one side and violet on the other.
- Familiar examples of chromatic dispersion are when white light strikes a prism or raindrops and a rainbow of colours becomes visible to an observer.
The spectral colour model represents the range of pure colours that correspond to specific wavelengths of visible light. These colours are called spectral colours because they are not created by mixing other colours but are produced by a single wavelength of light. This model is important because it directly reflects how human vision perceives light that comes from natural sources, like sunlight, which contains a range of wavelengths.
- The spectral colour model is typically represented as a continuous strip, with red at one end (longest wavelength) and violet at the other (shortest wavelength).
- Wavelengths and Colour Perception: In the spectral colour model, each wavelength corresponds to a distinct colour, ranging from red (with the longest wavelength, around 700 nanometres) to violet (with the shortest wavelength, around 400 nanometres). The human eye perceives these colours as pure because they are not the result of mixing other wavelengths.
- Pure Colours: Spectral colours are considered “pure” because they are made up of only one wavelength. This is in contrast to colours produced by mixing light (like in the RGB colour model) or pigments (in the CMY model), where a combination of wavelengths leads to different colours.
- Applications: The spectral colour model is useful in understanding natural light phenomena like rainbows, where each visible colour represents a different part of the light spectrum. It is also applied in fields like optics to describe how the eye responds to light in a precise, measurable way.
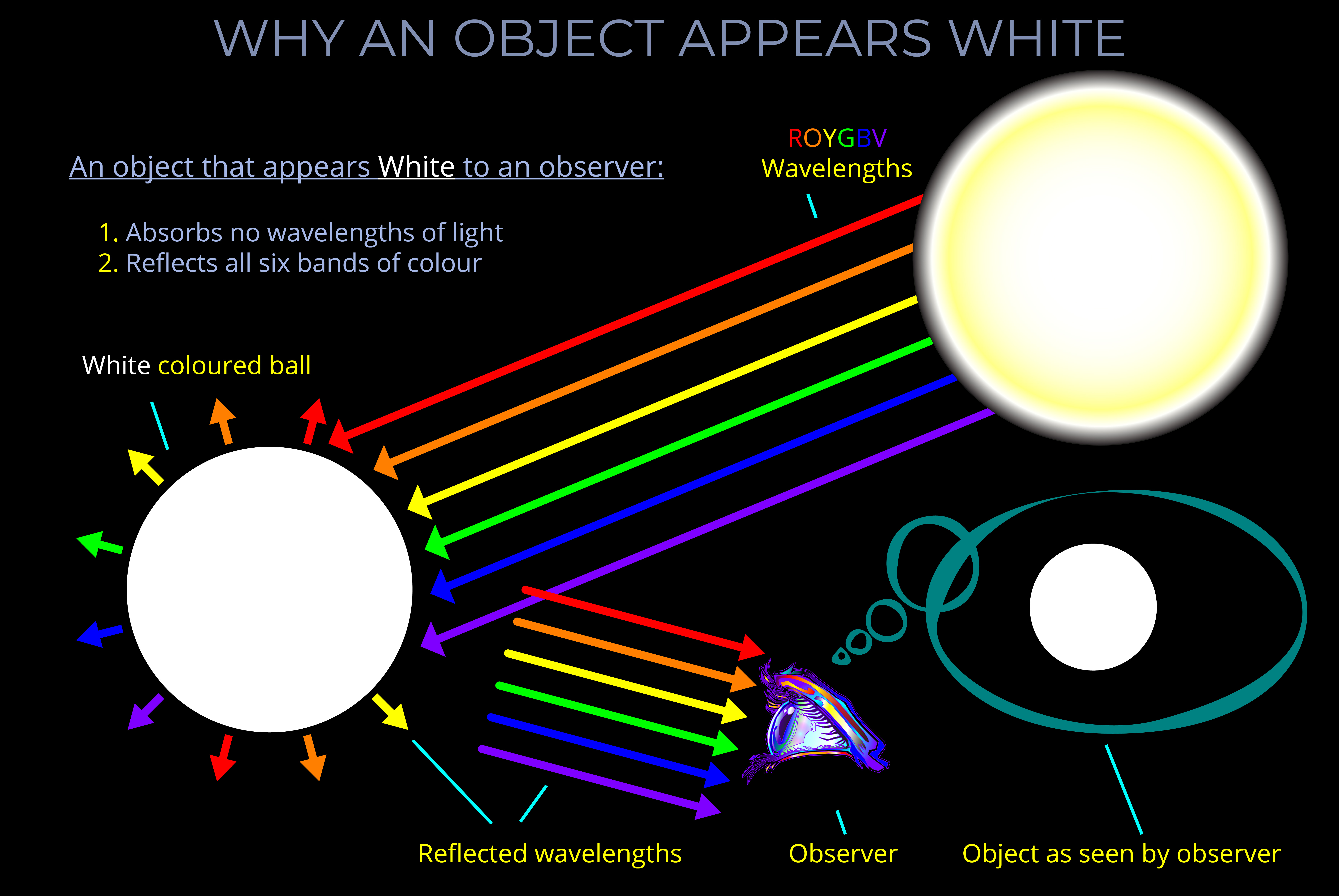
White light is the term for visible light that contains all wavelengths of the visible spectrum at equal intensities.
- The sun emits white light because sunlight contains all the wavelengths of the visible spectrum in roughly equal proportions.
- Light travelling through a vacuum or a medium is termed white light if it includes all wavelengths of visible light.
- Light travelling through a vacuum or air is not visible to our eyes unless it interacts with something.
- The term white light can have two meanings:
- It can refer to a combination of all wavelengths of visible light travelling through space, regardless of observation.
- What a person sees when all colours of the visible spectrum hit a white or neutral-coloured surface.
Total internal reflection occurs when light travelling through a denser medium strikes a boundary with a less dense medium at an angle exceeding a specific critical angle. As a result, all the light is reflected back into the denser medium, and no light transmits into the second medium.
- Total Internal reflection only takes place when the first medium (where the light originates) is denser than the second medium.
- The critical angle is the angle of incidence above which total internal reflection occurs.
- The critical angle is measured with respect to the normal.
- The normal is an imaginary line drawn in a ray diagram perpendicular to, so at a right angle to (900), to the boundary between two media.
- The observer effect is a principle of physics and states that any interaction between a particle and a measuring device will inevitably change the state of the particle. This is because the act of measurement itself imposes a disturbance on the particle’s wave function, which is the mathematical description of its state.
- The concept of observation refers to the act of engaging with an electron or other particle, achieved through measuring its position or momentum.
- In the context of quantum mechanics, observation isn’t a passive undertaking, observation actively alters a particle’s state.
- This means that any kind of interaction with an atom, or with one of its constituent particles, that provides insight into its state results in a change to that state. The act of observation is always intrusive and will always change the state of the object being observed.
- It can be challenging to reconcile this with our daily experience, where we believe we can observe things without inducing any change in them.
Internal reflection occurs when light travelling through a medium, such as water or glass, reaches the boundary with another medium, like air, and a portion of the light reflects back into the original medium. This happens regardless of the angle of incidence, as long as the light encounters the boundary between the two media.
- Internal reflection is a common phenomenon not only for visible light but for all types of electromagnetic radiation. For internal reflection to occur, the refractive index of the second medium must be lower than that of the first medium. This means internal reflection happens when light moves from a denser medium, such as water or glass, to a less dense medium, like air, but not when light moves from air to glass or water.
- In everyday situations, light is typically both refracted and reflected at the boundary between water or glass and air, often due to irregularities on the surface. If the angle at which light strikes this boundary is less than the critical angle, the light is refracted as it crosses into the second medium.
- When light strikes the boundary exactly at the critical angle, it neither fully reflects nor refracts but travels along the boundary between the two media. However, if the angle of incidence exceeds the critical angle, the light will undergo total internal reflection, meaning no light passes through, and all of it is reflected back into the original medium.
- The critical angle is the specific angle of incidence, measured with respect to the normal (a line perpendicular to the boundary), above which total internal reflection occurs.
- In ray diagrams, the normal is an imaginary line drawn perpendicular to the boundary between two media, and the angle of refraction is measured between the refracted ray and the normal. If the boundary is curved, the normal is drawn perpendicular to the curve at the point of incidence.
Reflection is the process where light rebounds from a surface into the medium it came from, instead of being absorbed by an opaque material or transmitted through a transparent one.
- The three laws of reflection are as follows:
- When light hits a reflective surface, the incoming light, the reflected light, and an imaginary line perpendicular to the surface (called the “normal line”) are all in the same flat area.
- The angle between the incoming light and the normal line is the same as the angle between the reflected light and the normal line. In other words, light bounces off the surface at the same angle as it came in.
- The incoming and reflected light are mirror images of each other when looking along the normal line. If you were to fold the flat area along the normal line, the incoming light would line up with the reflected light.