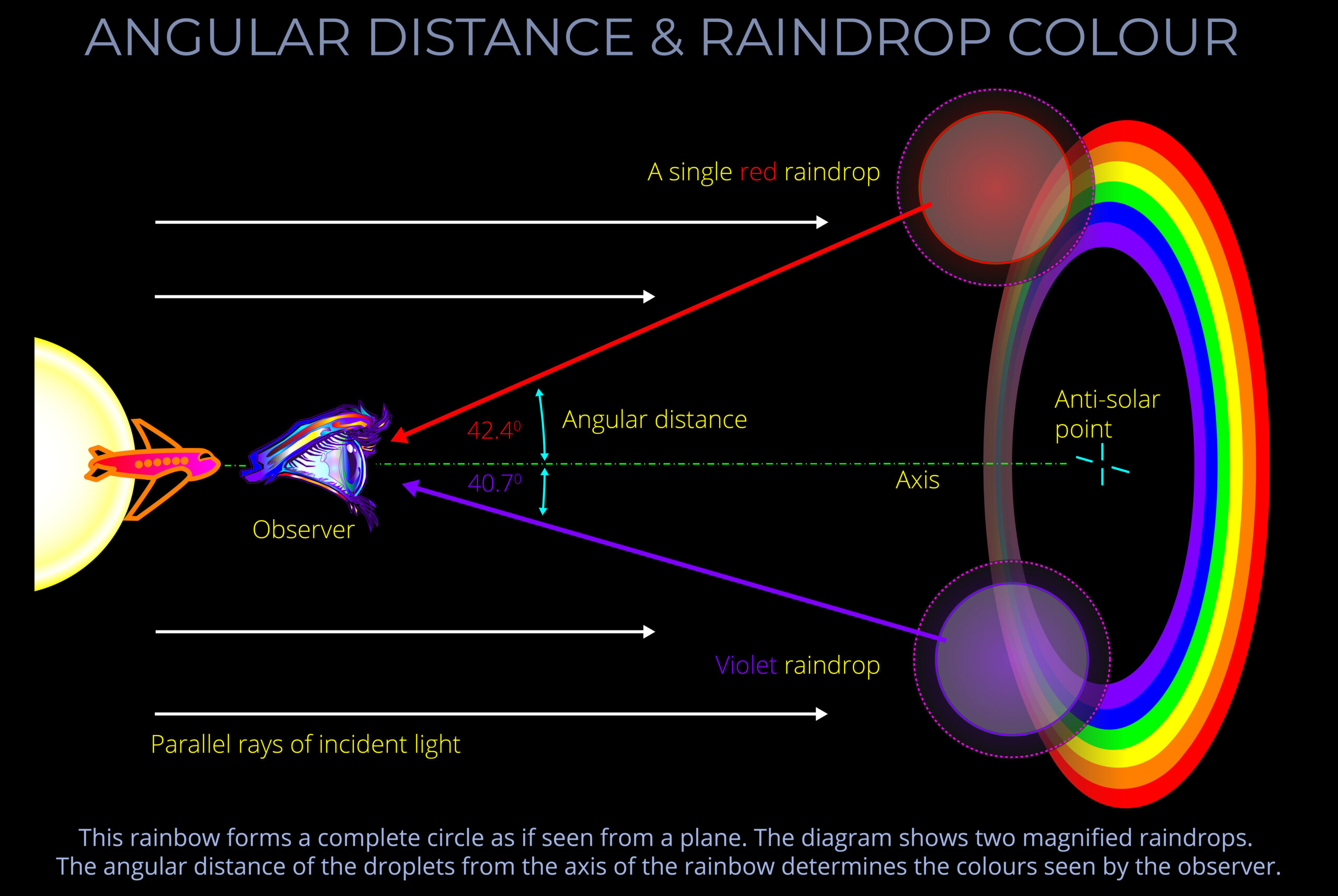
When discussing rainbows, angular distance is the angle between the line from the observer to the centre of the rainbow (rainbow axis) and the line from the observer to a specific colour within the arc of a rainbow.
- Angular distance, viewing angle, and angle of deflection are related concepts that produce similar values, expressed in degrees.
- Angular distance is one of the angles measured on a ray-tracing diagram that illustrates the sun, an observer, and a rainbow from a side view.
- Think of angular distance as the angle between the line to the centre of a rainbow down which an observer looks and the line to a specific colour in its arc. The red light is deviated by about 42.4° and violet light by about 40.7°.
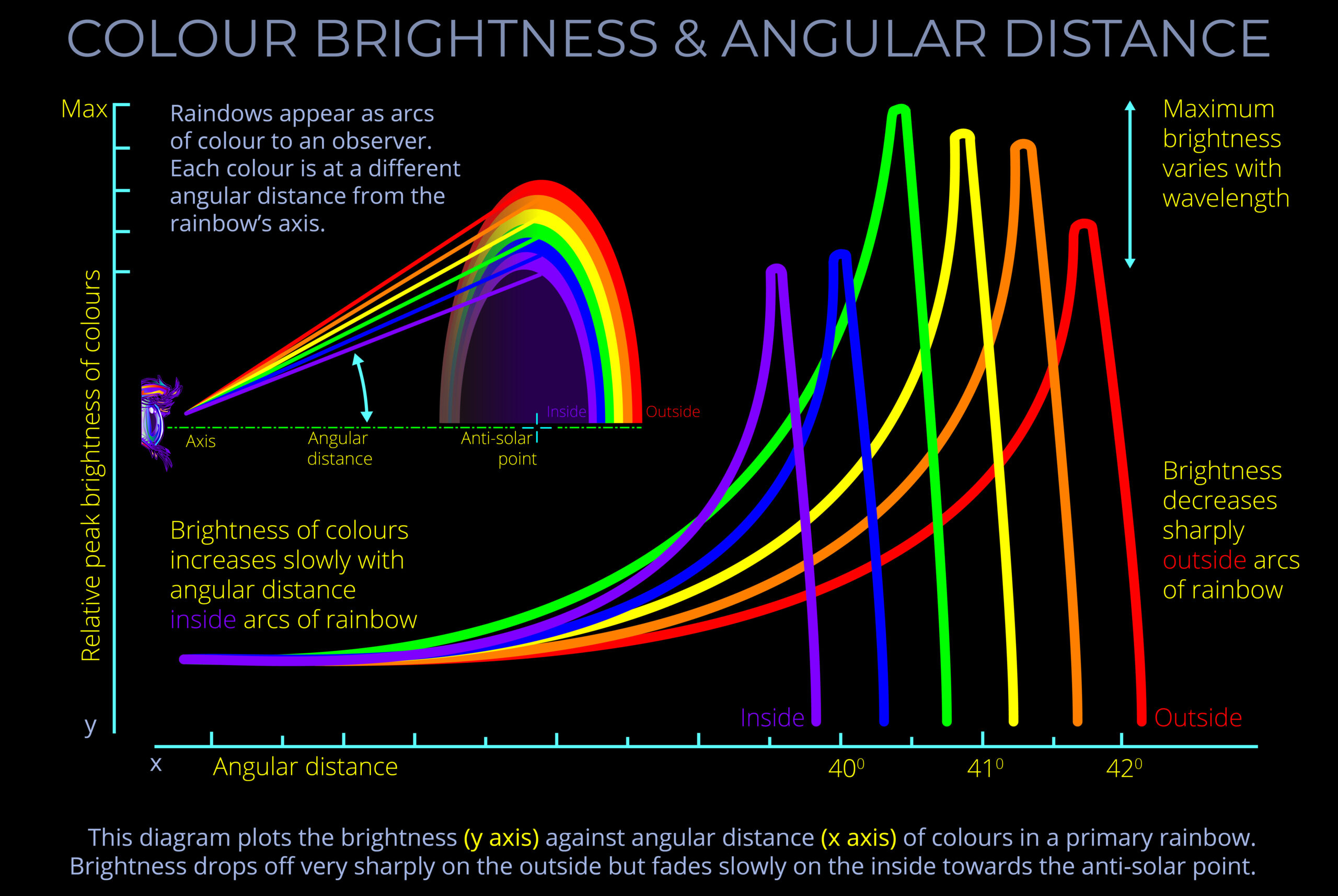
- Angular distances for different colours are fairly constant, determined by the laws of refraction and reflection inside the water droplets.
- The sun’s position, the observer’s location, and the specific location of rainfall all influence where a rainbow will appear from an observer’s perspective.
- The coloured arcs of a rainbow form parts of circles (discs or cones), and all these circles share a common centre—the observer’s anti-solar point, which is directly opposite the sun.
- The angular distance to a specific colour is consistent, regardless of the point chosen along the arc of that colour in the rainbow.
- The angular distance for any observed colour in a primary rainbow varies from approximately 42.4° for red to 40.7° for violet.
- The angular distance for any observed colour in a secondary rainbow ranges from about 53.4° for red to 50.4° for violet, measured from the antisolar point.
- The angular distance for any specific colour within a rainbow can indeed be calculated, depending on its wavelength and how it refracts within the water droplets.
- From an observer’s viewpoint, all the incoming light rays seen by the observer appear parallel to each other as they approach a raindrop.
- Most of the observable incident rays that strike a raindrop follow paths that place them outside the range of possible viewing angles. The unobserved rays are all deflected towards the centre of a rainbow.
- Many of the light rays that strike a raindrop follow paths that place them outside the range of possible viewing angles, so do contribute to the coloured arcs seen by an observer.
About viewing angles, angular distance and angles of deflection
- The term viewing angle refers to the angle, measured in degrees, between the direction an observer looks in to see the centre of the rainbow and the direction they look to see a specific colour within the rainbow’s arc.
- The term angular distance refers to the same measurement as the viewing angle, especially when depicted on a side elevation diagram.
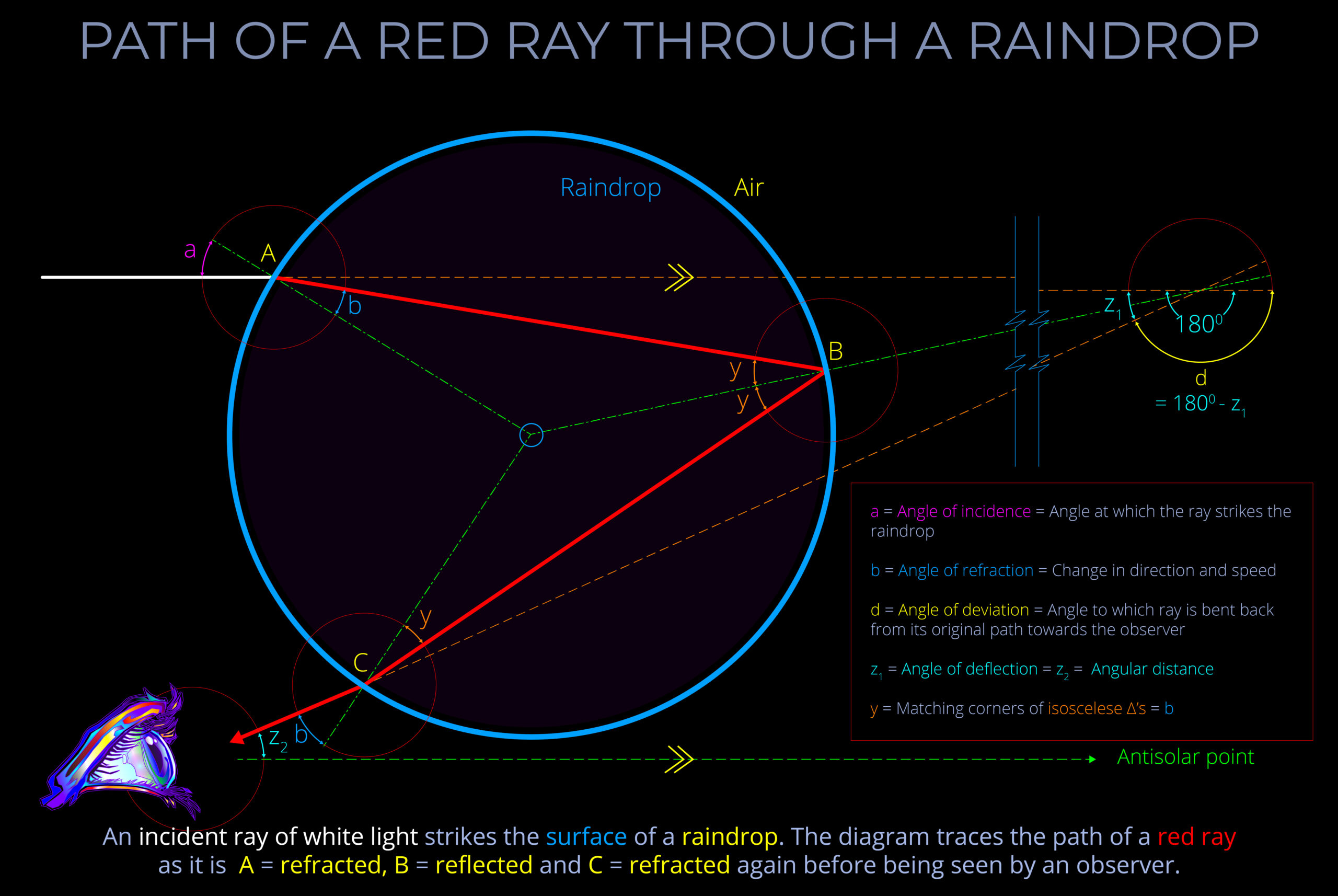
- The angle of deflection measures the change in direction that a light ray undergoes as it strikes, refracts into, reflects inside, and refracts out of a raindrop towards an observer.
- The term rainbow ray refers to the path taken by a deflected light ray that results in the most intense colour perception for a specific wavelength of light passing through a raindrop.
- The term angle of deviation measures the change in direction a light ray undergoes due to refraction and reflection inside a raindrop, relative to its original direction towards an observer.
- In any specific case of a light ray passing through a raindrop, the angle of deviation and the angle of deflection are interrelated and their sum equals 1800.
- The angle of deviation is equal to 1800 minus the angle of deflection, and vice versa, so the angle of deflection is equal to 1800 minus the angle of deviation.
- In any specific instance, the angle of deflection is approximately the same as the viewing angle, because the incident light rays that contribute to a rainbow all approach parallel to the axis of the rainbow.
Related diagrams
Each diagram below can be viewed on its own page with a full explanation.
