If one line is normal to another, then it is at right angles to it.
In geometry, normal (a or the normal) refers to a line drawn perpendicular to a given line, plane or surface.
- How a normal appears in a geometric drawing depends on the circumstances:
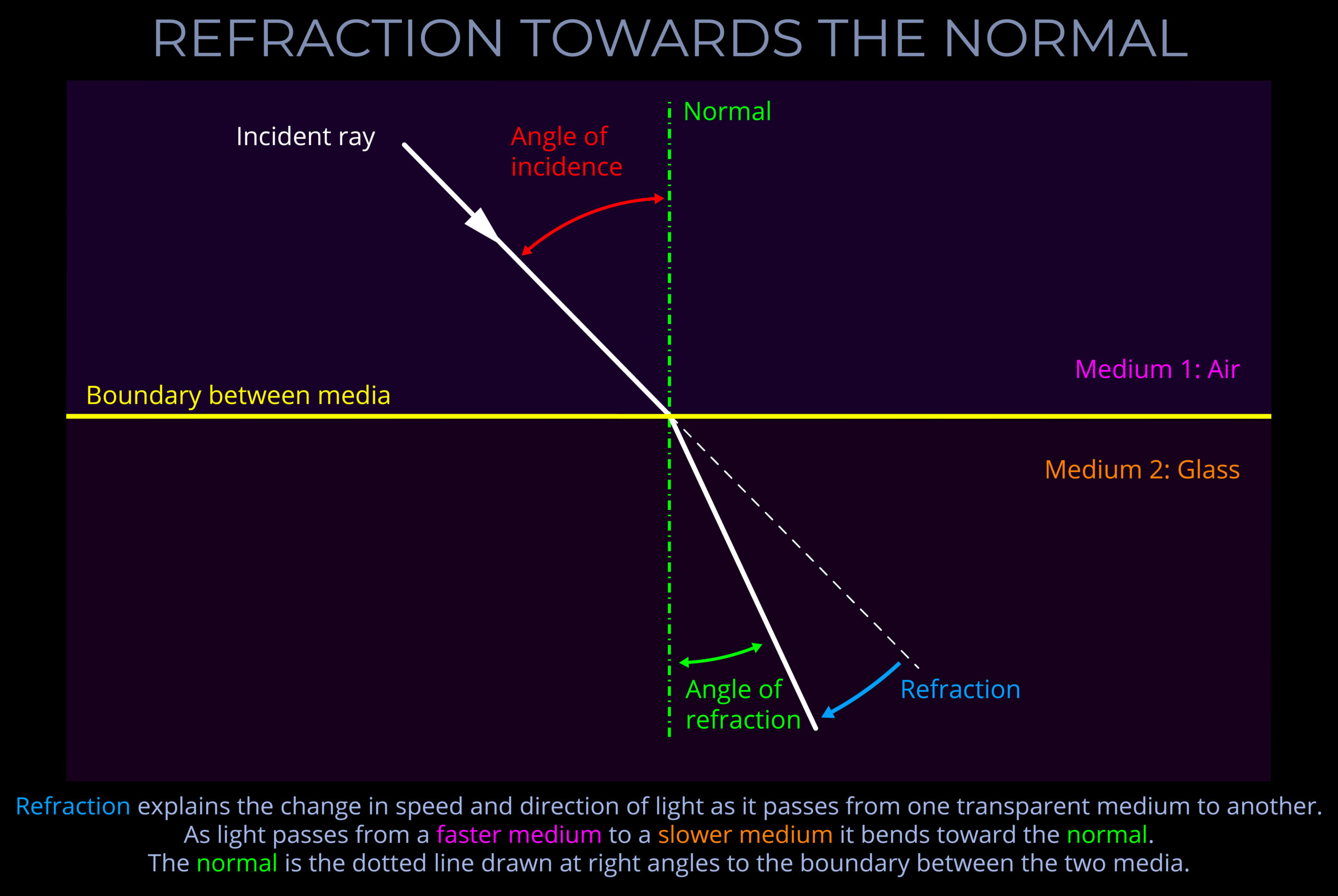
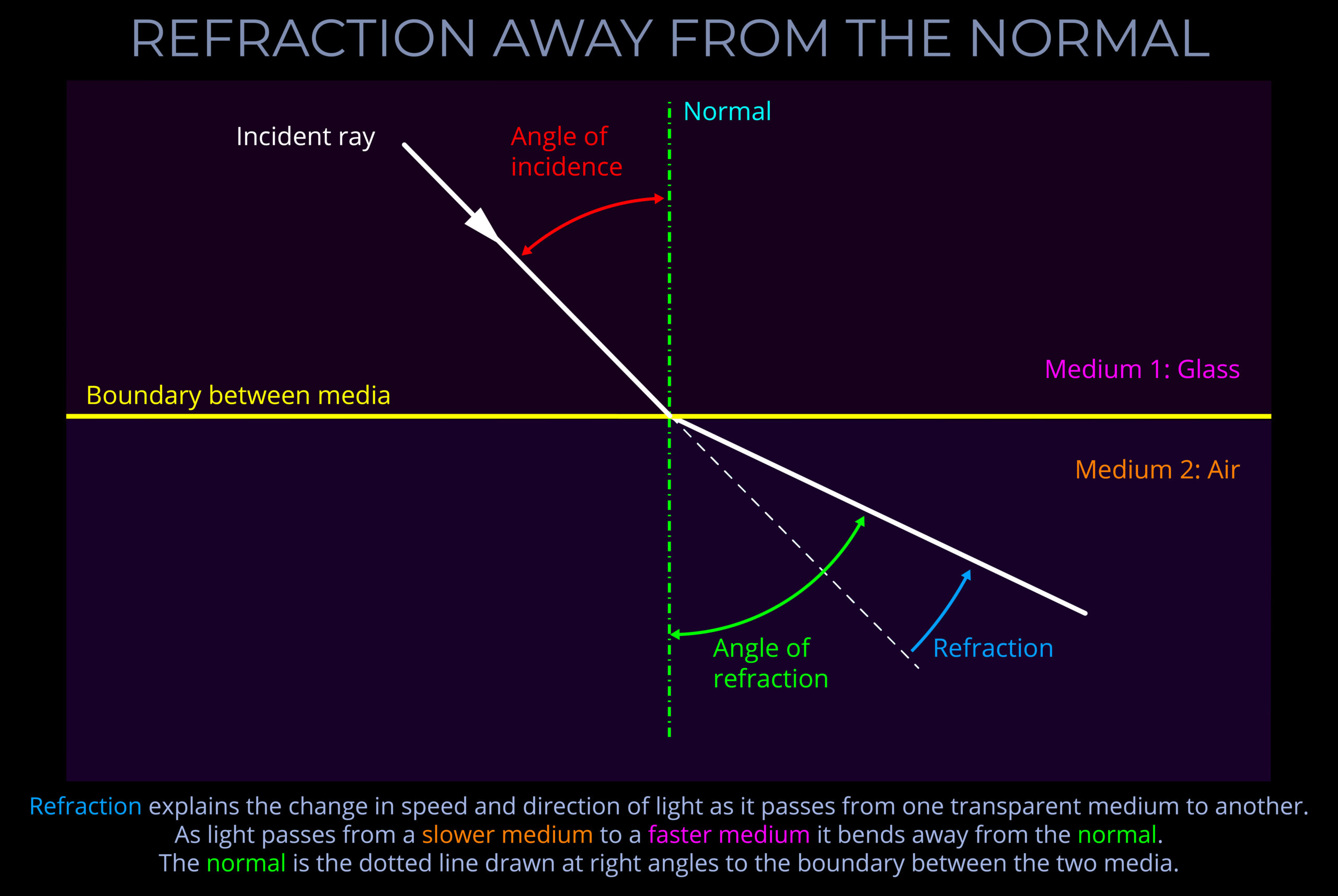
- When light strikes a flat surface or plane, or the boundary between two surfaces, the normal is drawn perpendicular to the surface, forming a right angle (90°) with it.
- Expressed more formally, in optics, the normal is a geometric construct, a line drawn perpendicular to the interface between two media at the point of contact. This conceptually defined reference line is crucial for characterizing various light-matter interactions, such as reflection, refraction, and absorption.
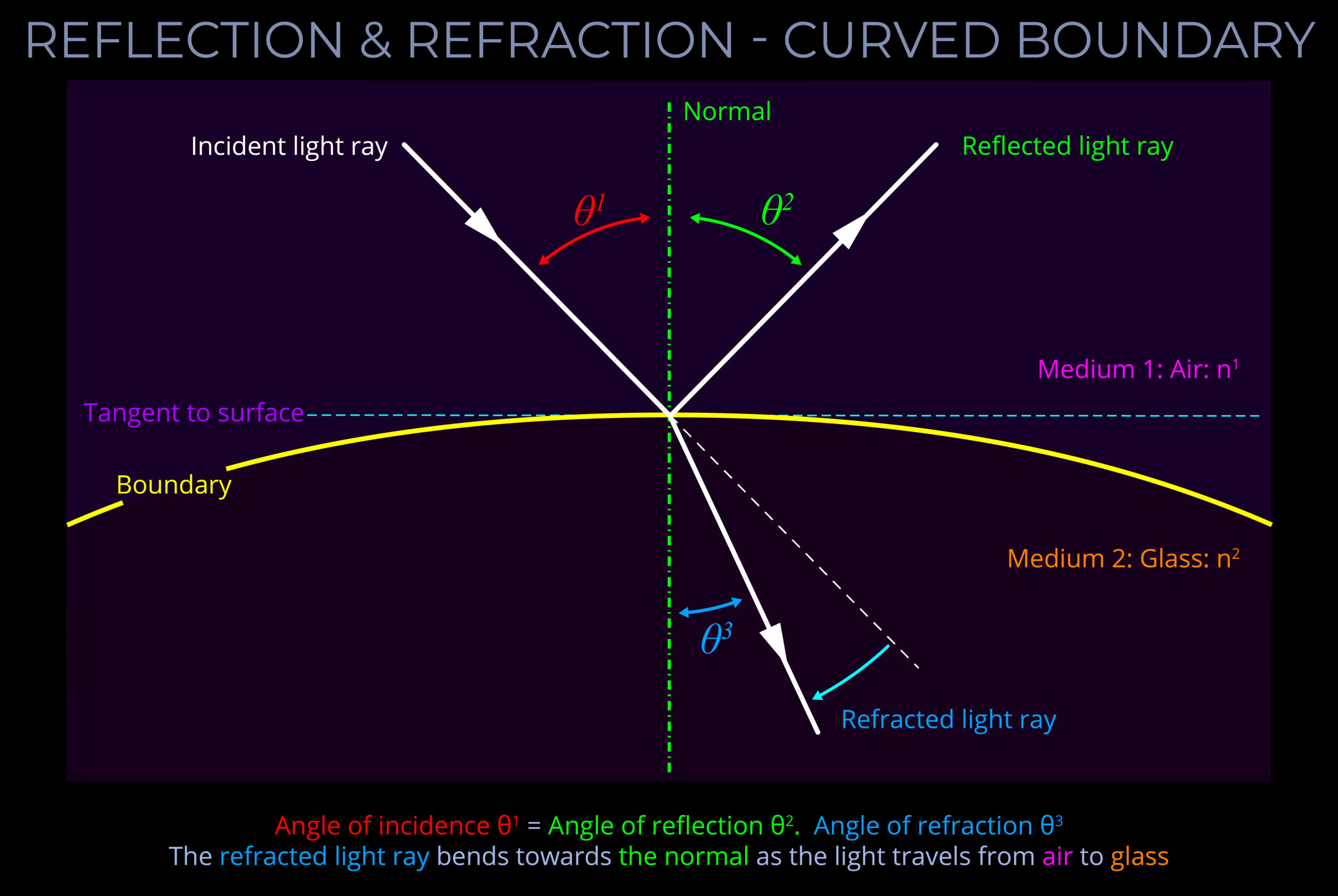
- When dealing with curved surfaces, such as those found on spheres or other three-dimensional objects, determining the normal requires a slightly different approach. Instead of simply drawing a line perpendicular to the surface as with a flat plane, draw the normal straight up from the point where light hits the surface.
- Similarly, when considering the centre of a sphere, the normal line passes through the centre of the sphere. This is because, regardless of where light enters or exits the sphere, the normal represents the direction perpendicular to the surface at that point.
Remember that:
- Light travels in a straight line through a vacuum or a transparent medium such as air, glass, or water that is still or in a constant state of motion.
- When light encounters an obstacle or passes from one transparent medium to another, it can result in a variety of optical phenomena including absorption, dispersion, diffraction, polarization, reflection, refraction, scattering, or transmission.
- Geometry can be used to calculate the outcome of light encountering different optical phenomena, such as the angle of refraction or reflection.
- When a normal is drawn on a ray-tracing diagram, it provides a reference perpendicular to the surface against which changes in direction of light can be measured.
Related diagrams
Each diagram below can be viewed on its own page with a full explanation.
- If one line is normal to another, then it is at right angles to it.
- In geometry, normal (a or the normal) refers to a line drawn perpendicular to a given line, plane or surface.
- How a normal appears in a geometric drawing depends on the circumstances:
- When light strikes a flat surface or plane, or the boundary between two surfaces, the normal is drawn perpendicular to the surface, forming a right angle (90°) with it.
- Expressed more formally, in optics, the normal is a geometric construct, a line drawn perpendicular to the interface between two media at the point of contact. This conceptually defined reference line is crucial for characterizing various light-matter interactions, such as reflection, refraction, and absorption.
- When dealing with curved surfaces, such as those found on spheres or other three-dimensional objects, determining the normal requires a slightly different approach. Instead of simply drawing a line perpendicular to the surface as with a flat plane, draw the normal straight up from the point where light hits the surface.
- Similarly, when considering the centre of a sphere, the normal line passes through the centre of the sphere. This is because, regardless of where light enters or exits the sphere, the normal represents the direction perpendicular to the surface at that point.