Refractive Index Explained
£0.00
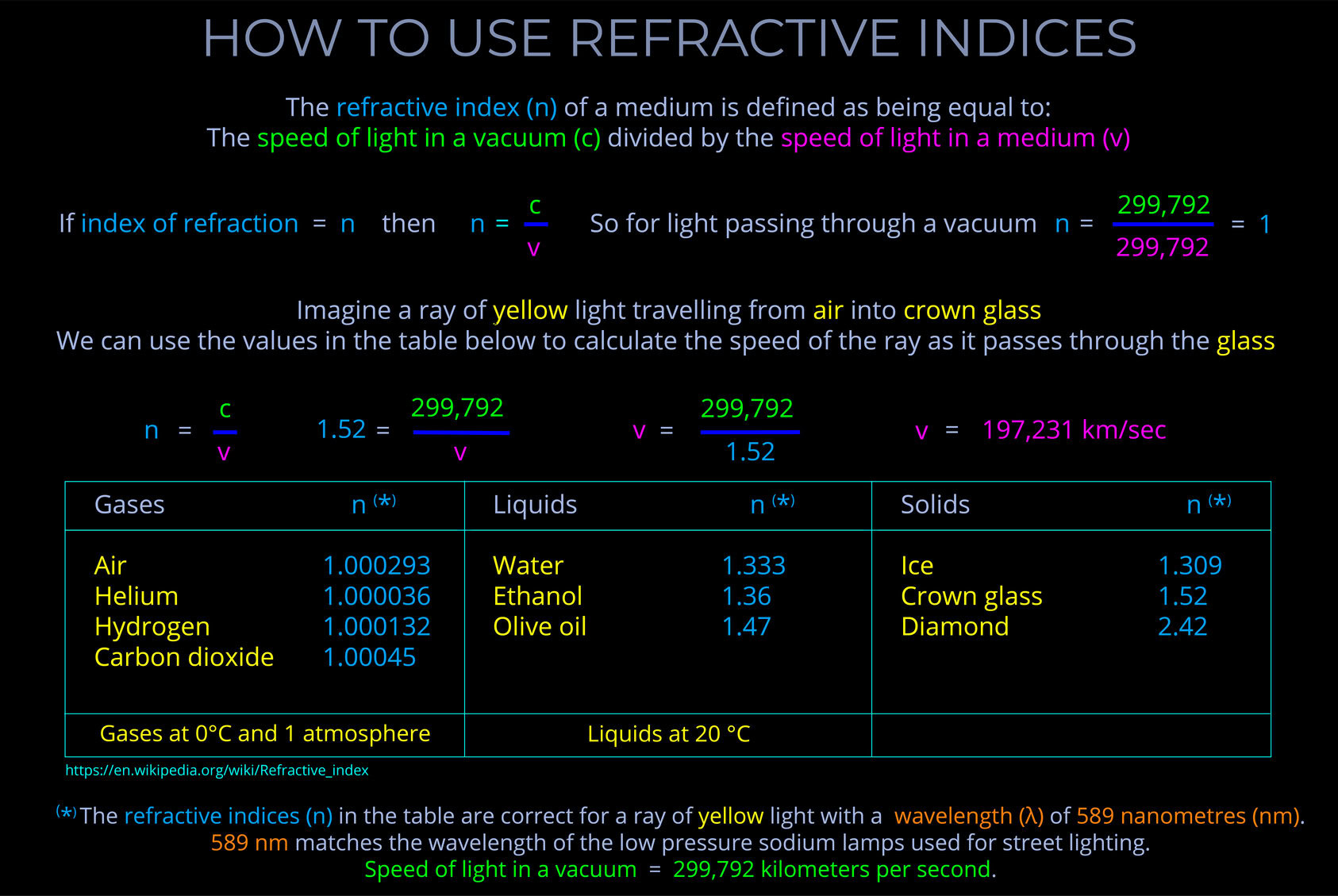
The diagram demonstrates the direct relationship between the speed of light as it travels through a vacuum (c) and the speed of light as it travels through any other transparent medium (v).
- Because the speed of light in a vacuum is always the same, the formula can be used to calculate:
- The refractive index (n) of a medium if the speed of light through the medium (v) is known.
- The speed of light in a medium (v) if its refractive index (n) is known
Description
Refractive Index Explained
TRY SOME QUICK QUESTIONS AND ANSWERS TO GET STARTED
About the diagram
Have you already checked out An Introduction to Reflection, Refraction and Dispersion?
It is the opening page of our Reflection, Refraction and Dispersion Series and contains masses of useful information. This is the table of contents:
Overview of this page
- This page explains what is meant by the refractive index of a medium (also called the index of refraction).
- Related terms, including reflection, refraction and chromatic dispersion are covered on earlier pages of this series.
- An introduction to the law of refraction (sometimes called Snell’s law) also appears in the series.
An overview of refraction
- Refraction refers to the way that light (electromagnetic radiation) changes speed and direction as it travels from one transparent medium into another.
- Refraction takes place as light travels across the boundary between different transparent media and is a result of their different optical properties.
- Refraction is the result of the differences in the optical density of transparent media. Gases have a very low optical density whilst diamonds have a high optical density.
- When light is refracted its path bends and so changes direction.
- The effect of refraction on the path of a ray of light is measured by the difference between the angle of incidence and the angle of reflection.
- As light travels across the interface between different media it changes speed.
- Depending on the media through which light is refracted, its speed can either increase or decrease.
An overview of refraction and wavelength
- Every wavelength of light is affected to a different degree when it encounters a medium and undergoes refraction.
- Every wavelength of light changes both speed and direction by a different amount when it encounters a new medium and undergoes refraction.
- The change in angle for any wavelength of light undergoing refraction within a specific transparent medium can be predicted if the refractive index of the medium is known.
- The refractive index for a medium is calculated by finding the difference between the speed of light in a vacuum and its speed as it travels through the medium.
| Colour | wavelength (nm) | Refractive index |
|---|---|---|
| Red | 640 | 1.50917 |
| Yellow | 589 | 1.51124 |
| Green | 509 | 1.51534 |
| Blue | 486 | 1.51690 |
| Violet | 434 | 1.52136 |
The refractive index for crown glass is often given as being 1.52. This table shows how that figure might alter with wavelength
The diagram
- The refractive index of a medium (sometimes called the index of refraction) is used to calculate the change in speed or direction as light travels from one transparent medium into another.
- The equation can be applied to any situation where the optical properties of a specific transparent medium are being investigated.
- The refractive index is used in the design, manufacture and use of prisms, lenses, optical tools and optical equipment of all types.
- The equation in the diagram demonstrates the direct relationship between the speed of light as it travels through a vacuum (c), the speed of light as it travels through any other transparent medium (v) and the refractive index of a medium (n).
- Because the speed of light in a vacuum is always the same, the formula can be used to calculate:
- The refractive index (n) of a medium if the speed of light through the medium (v) is known.
- The speed of light in a medium (v) if its refractive index (n) is known.
- The refractive index of a material (n) can also be used to predict the change of direction of a light ray as it crosses the boundary between transparent media (see Snell’s law of refraction).
- The diagram identifies the symbols commonly used for refractive index (n), speed of light in a vacuum (c) and speed of light of a medium (v).
- At the bottom of the diagram, the characteristics of optically dense and optically rare media are explained.
Remember:
- The speed of light in a vacuum is always 299,792 kilometres per second.
- A vacuum is an empty space, and because there is nothing to obstruct it, light travels through it at its maximum speed.
- The speed of light in any other medium is less than 299,792 km/sec.
- In the right conditions, transparent media cause incident light to change direction and to disperse into their component colours.
- When light is refracted and changes direction, the angle is determined by the refractive index of the medium it enters.
- Only a narrow range of wavelengths that form the full electromagnetic spectrum are visible to the human eye.
- The wavelengths that we can see are known as the visible spectrum.
- The presence of different wavelengths of light around us results in the colours we see in the world.
Refractive index
- The refractive index (also known as the index of refraction) of a transparent medium allows the path of refracted light through a transparent medium to be calculated.
- The refractive index is a ratio calculated by dividing the change in the speed of light in a vacuum by its speed as it travels through a specific medium.
- The refractive index of a medium can be calculated using the formula:
n = refractive index, c = speed of light in a vacuum, v = speed of light in a transparent medium
- When light travels through a vacuum, such as outer space, it travels at its maximum speed of 299,792 kilometres per second.
- When light travels through any other transparent medium it travels more slowly.
- Refractive indices describe the ratio between the speed of light in a vacuum and the speed of light in another medium.
- Most transparent media have a refractive index of between 1.0 and 2.0.
- Whilst the refractive index of a vacuum has the value of 1.0, the refractive index of water is 1.333.
- The ratio between them is therefore 1:1.333
- A simple example of a ratio is of mixing concrete using 1 part of cement to 2 part of sand. The ratio is expressed as 1:2.
- If we divide the refractive index for light travelling through a vacuum (1.0) by the refractive index for glass (1.333) we find that light travels at 75% of the speed of light in a vacuum.
For an explanation of the refractive index (index of refraction) of a medium see: Refractive Index Explained.
For an explanation of the Law of Refraction see: Snell’s Law of Refraction Explained.
Some key terms
The refractive index (index of refraction) of a medium measures how much the speed of light is reduced when it passes through a medium compared to its speed in a vacuum.
- Refractive index (or, index of refraction) is a measurement of how much the speed of light is reduced when it passes through a medium compared to the speed of light in a vacuum.
- The concept of refractive index applies to the full electromagnetic spectrum, from gamma-rays to radio waves.
- The refractive index can vary with the wavelength of the light being refracted. This phenomenon is called dispersion, and it is what causes white light to split into its constituent colours when it passes through a prism.
- The refractive index of a material can be affected by various factors such as temperature, pressure, and density.
A nanometre (nm) is a unit of length in the metric system, equal to one billionth of a metre (1 nm = 1 × 10⁻⁹ metres). It is commonly used to measure extremely small distances, particularly at the atomic and molecular scale.
- In the context of light and electromagnetic radiation, a nanometre is often used to describe wavelengths of visible light.
The wavelength of visible light ranges from about 700 nm (red) to 400 nm (violet). - Nanometres are also used to measure components like the thickness of materials, the size of particles in nanotechnology, and the spacing between atoms in a crystal lattice.
The refractive index (index of refraction) of a medium measures how much the speed of light is reduced when it passes through a medium compared to its speed in a vacuum.
- Refractive index (or, index of refraction) is a measurement of how much the speed of light is reduced when it passes through a medium compared to the speed of light in a vacuum.
- The concept of refractive index applies to the full electromagnetic spectrum, from gamma-rays to radio waves.
- The refractive index can vary with the wavelength of the light being refracted. This phenomenon is called dispersion, and it is what causes white light to split into its constituent colours when it passes through a prism.
- The refractive index of a material can be affected by various factors such as temperature, pressure, and density.
In physics and optics, a medium refers to any material through which light or other electromagnetic waves can travel. It’s essentially a substance that acts as a carrier for these waves.
- Light is a form of electromagnetic radiation, which travels in the form of waves. These waves consist of oscillating electric and magnetic fields.
- The properties of the medium, such as its density and composition, influence how light propagates through it.
- Different mediums can affect the speed, direction, and behaviour of light waves. For instance, light travels slower in water compared to a vacuum.
- Examples of Mediums:
- Transparent: Materials like air, glass, and water allow most light to pass through, with minimal absorption or scattering. These are good examples of mediums for light propagation.
- Translucent: Some materials, like frosted glass or thin paper, partially transmit light. They allow some light to pass through while diffusing or scattering the rest.
- Opaque: Materials like wood or metal block light completely. They don’t allow any light to travel through them.
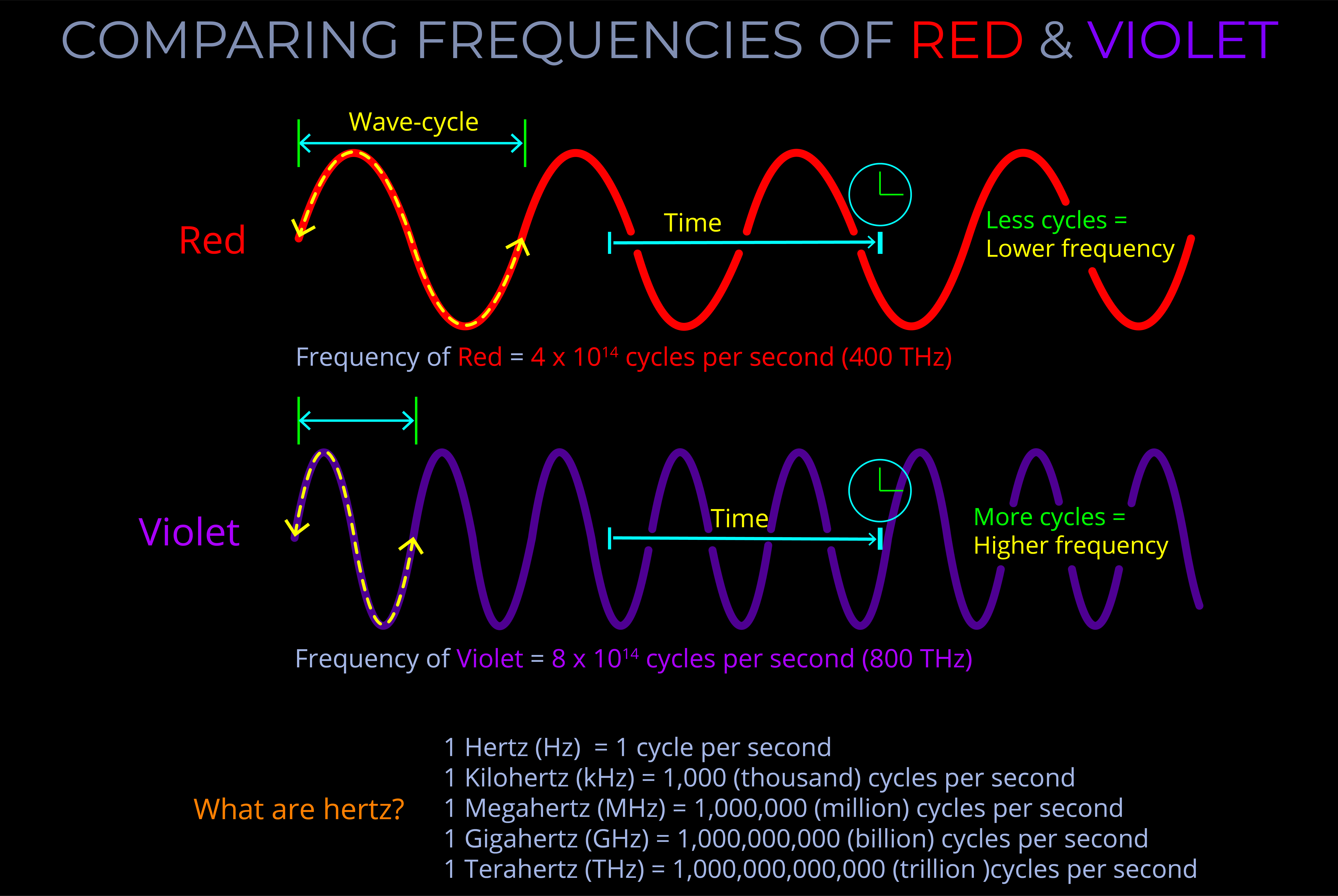
Wavelength measures a complete wave cycle, which is the distance from any point on a wave to the corresponding point on the next wave.
- While wavelength can be measured from any point on a wave, it is often simplest to measure from the peak of one wave to the peak of the next or from the bottom of one trough to the bottom of the next, ensuring the measurement covers the whole of the cycle.
- The wavelength of an electromagnetic wave is usually given in metres.
- The wavelength of visible light is typically measured in nanometres, with 1,000,000,000 nanometres making up a metre.
- Radio waves, visible light, and gamma waves for example, each have different ranges of wavelengths within the electromagnetic spectrum.
Optical density is a measure of how much a material resists and slows the transmission of light.
- The higher the optical density of a material, the slower light travels through it.
- The lower the optical density of a material, the faster light travels through it.
- A vacuum is not a medium and has zero optical density.
- Light travels through a vacuum at the maximum possible speed of light which is 299,792 kilometres per second.
- Optical density and refractive index are related properties.
- In general, materials with higher optical density tend to have higher refractive indices and vice versa.
- The greater the difference in refractive index between two materials, the more they will bend light when they come into contact.
Light travels at different speeds through various media, such as air, glass, or water. A “fast” medium is one where light moves more quickly compared to other materials.
- In a vacuum, light travels at 299,792 kilometres per second, but in other media, it slows down.
- In some cases, the speed is close to that in a vacuum, while in others, it is significantly slower.
- Knowing whether a medium is fast or slow helps predict how light will behave when it crosses from one medium to another.
- If light crosses from a fast medium to a slower one, it bends towards the normal.
- If light crosses from a slow medium to a faster one, it bends away from the normal.
- In optics, the normal is a line drawn perpendicular (at a 90° angle) to the boundary between two media in a ray diagram.
As light crosses the boundary between two transparent media, the law of refraction (Snell’s law) states the relationship between the angle of incidence and angle of refraction of the light with reference to the refractive indices of both media as follows:
When electromagnetic radiation (light) of a specific frequency crosses the interface of any given pair of media, the ratio of the sines of the angles of incidence and the sines of the angles of refraction is a constant in every case.
- Snell’s law deals with the fact that for an incident ray approaching the boundary of two media, the sine of the angle of incidence multiplied by the index of refraction of the first medium is equal to the sine of the angle of refraction multiplied by the index of refraction of the second medium.
- Snell’s law deals with the fact that the sine of the angle of incidence to the sine of the angle of refraction is constant when a light ray passes across the boundary from one medium to another.
- Snell’s law can be used to calculate the angle of incidence or refraction associated with the use of lenses, prisms and other everyday materials.
- When using Snell’s law:
- The angles of incidence and refraction are measured between the direction of a ray of light and the normal – where the normal is an imaginary line drawn on a ray diagram perpendicular to, so at a right angle to (900), to the boundary between two media.
- The wavelength of the incident light is accounted for.
- The refractive indices used are selected for the pair of media concerned.
- The speed of light is expressed in metres per second (m/s).
Refraction refers to the way that electromagnetic radiation (light) changes speed and direction as it travels across the boundary between one transparent medium and another.
- Light bends towards the normal and slows down when it moves from a fast medium (like air) to a slower medium (like water).
- Light bends away from the normal and speeds up when it moves from a slow medium (like diamond) to a faster medium (like glass).
- These phenomena are governed by Snell’s law, which describes the relationship between the angles of incidence and refraction.
- The refractive index (index of refraction) of a medium indicates how much the speed and direction of light are altered when travelling in or out of a medium.
- It is calculated by dividing the speed of light in a vacuum by the speed of light in the material.
- Snell’s law relates the angles of incidence and refraction to the refractive indices of the two media involved.
- Snell’s law states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is equal to the ratio of the refractive indices.
The speed (or velocity) of a light wave is a measurement of how far it travels in a certain time.
- The speed of light is measured in metres per second (m/s).
- Light travels through a vacuum at 300,000 kilometres per second.
- The exact speed at which light travels through a vacuum is 299,792,458 metres per second.
- Light travels through other media at lower speeds.
- A vacuum is a region of space that contains no matter.
- Matter is anything that has mass and occupies space by having volume.
- When discussing electromagnetic radiation the term medium (plural media) is used to refer to anything through which light propagates including empty space and any material that occupies space such as a solid, liquid or gas.
- In other contexts empty space is not considered to be a medium because it does not contain matter.