Dispersion of White Light in a Raindrop
£0.00
This is one of a set of almost 40 diagrams exploring Rainbows.
Each diagram appears on a separate page and is supported by a full explanation.
- Follow the links embedded in the text for definitions of all the key terms.
- For quick reference don’t miss the summaries of key terms further down each page.
Description
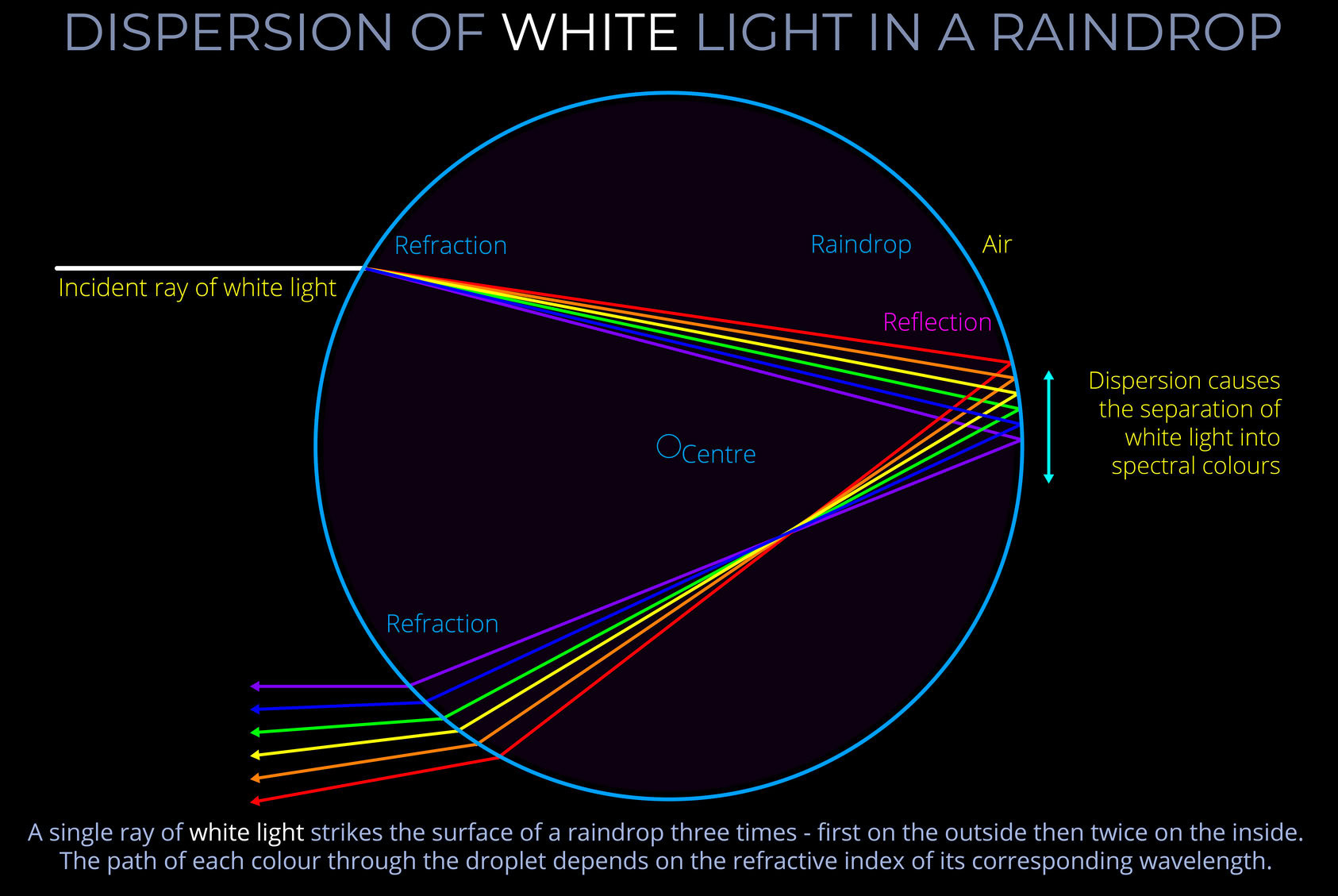
Dispersion of White Light in a Raindrop
TRY SOME QUICK QUESTIONS AND ANSWERS TO GET STARTED
About the diagram
Overview of raindrops
About the diagram
- The diagram provides a general picture of the combined effects of refraction and dispersion as white light is transmitted through a raindrop.
- White light refers to light that contains equal proportions of all wavelengths within the visible spectrum.
- The diagram shows the effect of refraction and chromatic dispersion on white light into spectral colours from red to violet.
- It is slight differences in the refractive index of water for different wavelengths of light that result in chromatic dispersion and the scattering of white light into rainbow colours.
- To delve a bit further into the diagram let’s go on to review the three key concepts, refraction, chromatic dispersion and scattering.
Chromatic dispersion
Scattering
Refraction
Some key terms
Refraction refers to the way that electromagnetic radiation (light) changes speed and direction as it travels across the boundary between one transparent medium and another.
- Light bends towards the normal and slows down when it moves from a fast medium (like air) to a slower medium (like water).
- Light bends away from the normal and speeds up when it moves from a slow medium (like diamond) to a faster medium (like glass).
- These phenomena are governed by Snell’s law, which describes the relationship between the angles of incidence and refraction.
- The refractive index (index of refraction) of a medium indicates how much the speed and direction of light are altered when travelling in or out of a medium.
- It is calculated by dividing the speed of light in a vacuum by the speed of light in the material.
- Snell’s law relates the angles of incidence and refraction to the refractive indices of the two media involved.
- Snell’s law states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is equal to the ratio of the refractive indices.
Incident light refers to light that is travelling towards an object or medium.
- Incident light refers to light that is travelling towards an object or medium.
- Incident light may come from the Sun, an artificial source or may have already been reflected off another surface, such as a mirror.
- When incident light strikes a surface or object, it may be absorbed, reflected, refracted, transmitted or undergo any combination of these optical effects.
- Incident light is typically represented on a ray diagram as a straight line with an arrow to indicate its direction of propagation.
Reflection is the process where light rebounds from a surface into the medium it came from, instead of being absorbed by an opaque material or transmitted through a transparent one.
- The three laws of reflection are as follows:
- When light hits a reflective surface, the incoming light, the reflected light, and an imaginary line perpendicular to the surface (called the “normal line”) are all in the same flat area.
- The angle between the incoming light and the normal line is the same as the angle between the reflected light and the normal line. In other words, light bounces off the surface at the same angle as it came in.
- The incoming and reflected light are mirror images of each other when looking along the normal line. If you were to fold the flat area along the normal line, the incoming light would line up with the reflected light.
The refractive index (index of refraction) of a medium measures how much the speed of light is reduced when it passes through a medium compared to its speed in a vacuum.
- Refractive index (or, index of refraction) is a measurement of how much the speed of light is reduced when it passes through a medium compared to the speed of light in a vacuum.
- The concept of refractive index applies to the full electromagnetic spectrum, from gamma-rays to radio waves.
- The refractive index can vary with the wavelength of the light being refracted. This phenomenon is called dispersion, and it is what causes white light to split into its constituent colours when it passes through a prism.
- The refractive index of a material can be affected by various factors such as temperature, pressure, and density.
Total internal reflection occurs when light travelling through a denser medium strikes a boundary with a less dense medium at an angle exceeding a specific critical angle. As a result, all the light is reflected back into the denser medium, and no light transmits into the second medium.
- Total Internal reflection only takes place when the first medium (where the light originates) is denser than the second medium.
- The critical angle is the angle of incidence above which total internal reflection occurs.
- The critical angle is measured with respect to the normal.
- The normal is an imaginary line drawn in a ray diagram perpendicular to, so at a right angle to (900), to the boundary between two media.
Internal reflection occurs when light travelling through a medium, such as water or glass, reaches the boundary with another medium, like air, and a portion of the light reflects back into the original medium. This happens regardless of the angle of incidence, as long as the light encounters the boundary between the two media.
- Internal reflection is a common phenomenon not only for visible light but for all types of electromagnetic radiation. For internal reflection to occur, the refractive index of the second medium must be lower than that of the first medium. This means internal reflection happens when light moves from a denser medium, such as water or glass, to a less dense medium, like air, but not when light moves from air to glass or water.
- In everyday situations, light is typically both refracted and reflected at the boundary between water or glass and air, often due to irregularities on the surface. If the angle at which light strikes this boundary is less than the critical angle, the light is refracted as it crosses into the second medium.
- When light strikes the boundary exactly at the critical angle, it neither fully reflects nor refracts but travels along the boundary between the two media. However, if the angle of incidence exceeds the critical angle, the light will undergo total internal reflection, meaning no light passes through, and all of it is reflected back into the original medium.
- The critical angle is the specific angle of incidence, measured with respect to the normal (a line perpendicular to the boundary), above which total internal reflection occurs.
- In ray diagrams, the normal is an imaginary line drawn perpendicular to the boundary between two media, and the angle of refraction is measured between the refracted ray and the normal. If the boundary is curved, the normal is drawn perpendicular to the curve at the point of incidence.
Visible light refers to the range of wavelengths of electromagnetic radiation that is perceived as colour by human observers. While the range of visible light is generally considered to be 400-700 nm, the exact range of colours perceptible can vary slightly between individuals.
- Visible light is one form of electromagnetic radiation. Other forms of electromagnetic radiation include radio waves, microwaves, infrared, ultraviolet, X-rays, and gamma rays. Visible light ranges from approximately 400 nanometres (nm) for violet to 700 nm for red.
- A human observer perceives visible light as a combination of all the spectral colours between red and violet, as well as a vast range of other colours produced from the blending of different wavelengths in varying proportions.
In the field of optics, dispersion is shorthand for chromatic dispersion which refers to the way that light, under certain conditions, separates into its component wavelengths, enabling the colours corresponding with each wavelength to become visible to a human observer.
- Chromatic dispersion refers to the dispersion of light according to its wavelength or colour.
- Chromatic dispersion is the result of the relationship between wavelength and refractive index.
- When light travels from one medium (such as air) to another (such as glass or water) each wavelength is refracted differently, causing the separation of white light into its constituent colours.
- When light undergoes refraction each wavelength changes direction by a different amount. In the case of white light, the separate wavelengths fan out into distinct bands of colour with red on one side and violet on the other.
- Familiar examples of chromatic dispersion are when white light strikes a prism or raindrops and a rainbow of colours becomes visible to an observer.
Visible light is the range of wavelengths of electromagnetic radiation perceived as colour by human observers.
- Visible light is a form of electromagnetic radiation.
- Other forms of electromagnetic radiation include radio waves, microwaves, infrared, ultraviolet, X-rays, and gamma rays.
- Visible light is perceived by a human observer as all the spectral colours between red and violet plus all other colours that result from combining wavelengths together in different proportions.
- A spectral colour is produced by a single wavelength of light.
- The complete range of colours that can be perceived by a human observer is called the visible spectrum.
- The range of wavelengths that produce visible light is a very small part of the electromagnetic spectrum.
As light crosses the boundary between two transparent media, the law of refraction (Snell’s law) states the relationship between the angle of incidence and angle of refraction of the light with reference to the refractive indices of both media as follows:
When electromagnetic radiation (light) of a specific frequency crosses the interface of any given pair of media, the ratio of the sines of the angles of incidence and the sines of the angles of refraction is a constant in every case.
- Snell’s law deals with the fact that for an incident ray approaching the boundary of two media, the sine of the angle of incidence multiplied by the index of refraction of the first medium is equal to the sine of the angle of refraction multiplied by the index of refraction of the second medium.
- Snell’s law deals with the fact that the sine of the angle of incidence to the sine of the angle of refraction is constant when a light ray passes across the boundary from one medium to another.
- Snell’s law can be used to calculate the angle of incidence or refraction associated with the use of lenses, prisms and other everyday materials.
- When using Snell’s law:
- The angles of incidence and refraction are measured between the direction of a ray of light and the normal – where the normal is an imaginary line drawn on a ray diagram perpendicular to, so at a right angle to (900), to the boundary between two media.
- The wavelength of the incident light is accounted for.
- The refractive indices used are selected for the pair of media concerned.
- The speed of light is expressed in metres per second (m/s).