Refractive Index of Water

$0.00

This is one of a set of almost 40 diagrams exploring Rainbows.

Each diagram appears on a separate page and is supported by a full explanation.

  • Follow the links embedded in the text for definitions of all the key terms.
  • For quick reference don’t miss the summaries of key terms further down each page.
SKU: N/A Categories: , Tags: , ,

Description

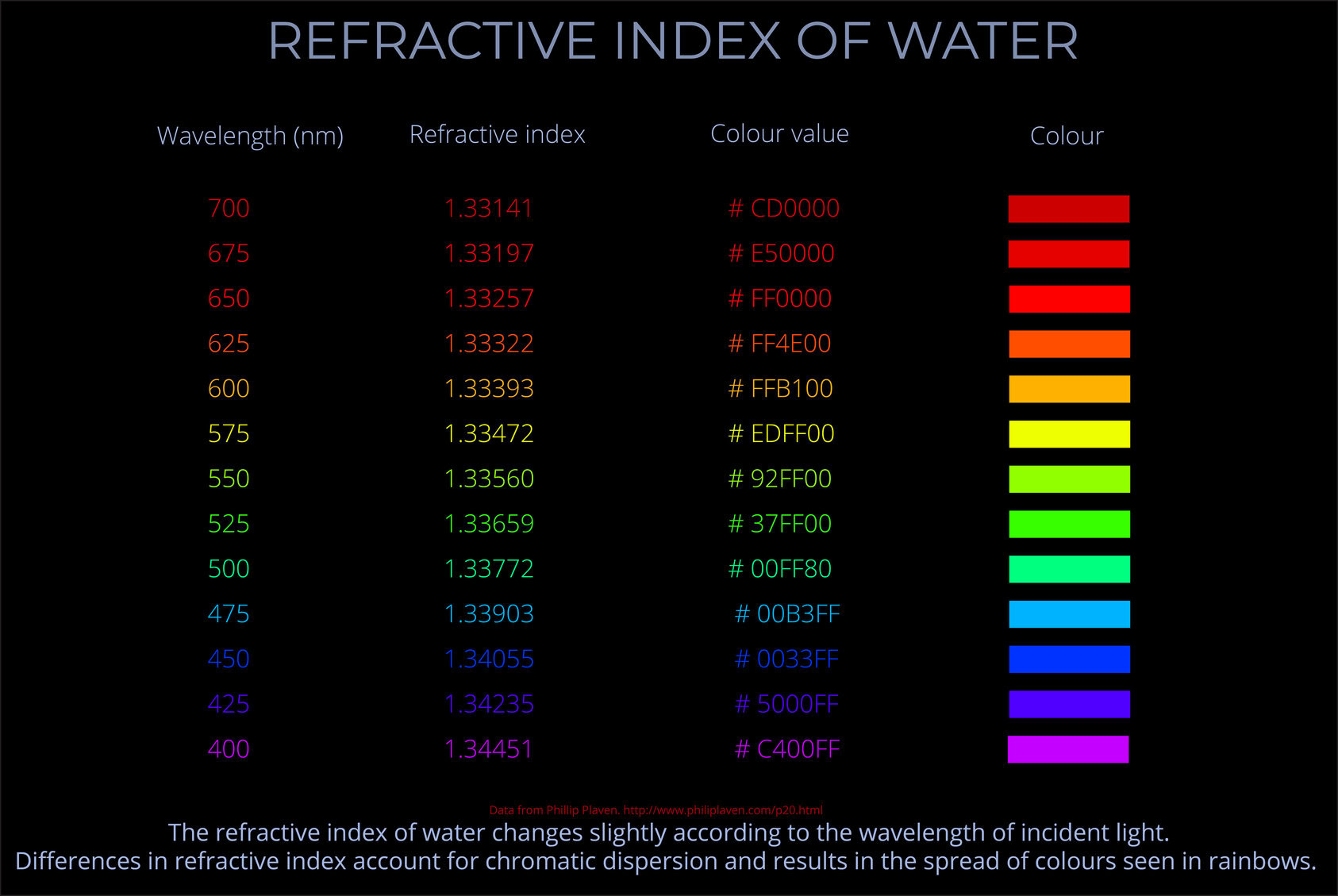
Refractive Index of Water

TRY SOME QUICK QUESTIONS AND ANSWERS TO GET STARTED
Is chromatic dispersion the result of refraction?
Yes! Light separates into different colours during the course of refraction.
How is chromatic dispersion related to refraction?
Every wavelength of light is affected to a different degree by the refractive index of a material and as a result changes direction by a different amount when passing from one medium (such as air) to another (such as glass or water).
What happens when light undergoes refraction?
As light travels from a fast medium such as air to a slow medium such as water it bends toward 'the normal' and slows down. As light passes from a slow medium such as diamond to a faster medium such as glass it bends away from 'the normal' and speeds up.
Does light undergo chromatic dispersion as it enters a raindrop?
Yes! Chromatic dispersion takes place as light crosses the boundary between one transparent medium and another if it has a different refractive index.
Does light undergo refraction as it travels across the boundary between one transparent medium into another?
Yes! When light leaves a vacuum or travels from one transparent medium into another, it undergoes refraction causing it to change both direction and speed.

About the diagram

About wavelength
About refractive index
About colour

Some key terms

Index of refraction

The refractive index (index of refraction) of a medium measures how much the speed of light is reduced when it passes through a medium compared to its speed in a vacuum.

  • Refractive index (or, index of refraction) is a measurement of how much the speed of light is reduced when it passes through a medium compared to the speed of light in a vacuum.
  • The concept of refractive index applies to the full electromagnetic spectrum, from gamma-rays to radio waves.
  • The refractive index can vary with the wavelength of the light being refracted. This phenomenon is called dispersion, and it is what causes white light to split into its constituent colours when it passes through a prism.
  • The refractive index of a material can be affected by various factors such as temperature, pressure, and density.
Refraction

Refraction refers to the way that electromagnetic radiation (light) changes speed and direction as it travels across the boundary between one transparent medium and another.

  • Light bends towards the normal and slows down when it moves from a fast medium (like air) to a slower medium (like water).
  • Light bends away from the normal and speeds up when it moves from a slow medium (like diamond) to a faster medium (like glass).
  • These phenomena are governed by Snell’s law, which describes the relationship between the angles of incidence and refraction.
  • The refractive index (index of refraction) of a medium indicates how much the speed and direction of light are altered when travelling in or out of a medium.
  • It is calculated by dividing the speed of light in a vacuum by the speed of light in the material.
  • Snell’s law relates the angles of incidence and refraction to the refractive indices of the two media involved.
  • Snell’s law states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is equal to the ratio of the refractive indices.
Refractive index

The refractive index (index of refraction) of a medium measures how much the speed of light is reduced when it passes through a medium compared to its speed in a vacuum.

  • Refractive index (or, index of refraction) is a measurement of how much the speed of light is reduced when it passes through a medium compared to the speed of light in a vacuum.
  • The concept of refractive index applies to the full electromagnetic spectrum, from gamma-rays to radio waves.
  • The refractive index can vary with the wavelength of the light being refracted. This phenomenon is called dispersion, and it is what causes white light to split into its constituent colours when it passes through a prism.
  • The refractive index of a material can be affected by various factors such as temperature, pressure, and density.

Diagrams are free to download

Downloads: Slides or Illustrations

DOWNLOAD DIAGRAMS
  • SLIDES are optimized for viewing on-screen.
  • ILLUSTRATIONS are optimized for printing on A4 pages in portrait format.
SLIDES
  • Slides are available in JPG and AI (Adobe Illustrator) file formats.
  • Titles: Slides have titles.
  • Backgrounds: Black.
  • Size: 1686 x 1124 pixels (3:2 aspect ratio).
ILLUSTRATIONS
  • Illustrations are available in JPG and AI two file formats.
  • Titles: No titles.
  • Backgrounds: White.
  • Size: 1686 x 1124 (3:2 aspect ratio). So all illustrations reproduce at the same scale when inserted into Word documents etc.
  • Labels: Calibri 24pt Italic.

File formats: JPG & AI

DOWNLOAD THE DIAGRAM ON THIS PAGE AS A JPG FILE
  • JPG (JPEG) diagrams are 1686 x 1124 pixels (3:2 aspect ratio).
  • If a JPG diagram doesn’t fit your needs, you can download it as an AI (Adobe Illustrator) file and edit it yourself.
  • JPG files can be placed or pasted directly into MS Office documents.
DOWNLOAD THE DIAGRAM ON THIS PAGE AS AN AI file
  • All AI (Adobe Illustrator) diagrams are 1686 x 1124 pixels (3:2 aspect ratio).
  • All our diagrams are created in Adobe Illustrator as vector drawings.
  • Save as or export AI files to other formats including PDF (.pdf), PNG (.png), JPG (.jpeg) and SVG(.svg) etc.

Spelling: UK & US

We use English (UK) spelling by default here at lightcolourvision.org.

COPY & PASTING TEXT
  • After copy/pasting text please do a spell-check to change our spelling to match your own document.
DOWNLOAD DIAGRAMS
  • Download AI versions of diagrams to change the spelling or language used for titles, labels etc.
  • We are adding American English (US) versions of diagrams on request. Just contact us and let us know what you need.
  • When downloading JPG versions of diagrams, look out for JPG (UK) or JPG (US) in the download dialogue box.

Download agreement

DOWNLOAD AGREEMENT

Light, Colour, Vision & How To See More (https://lightcolourvision.org) : Copyright © 2015-2022 : MediaStudies Trust.

Unless stated otherwise the author of all images and written content on lightcolourvision.org is Ric Mann.

ALL RIGHTS RESERVED

No part of this website may be copied, displayed, extracted, reproduced, utilised, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical or otherwise including but not limited to photocopying, recording, or scanning without the prior written permission of MediaStudies Trust.

EXCEPTIONS

Exceptions to the above statement are made for personal, educational and non-profit purposes:

Before downloading, cutting and pasting or reproducing any information, images or other assets found on lightcolourvision.org we ask you to agree to the following terms:

  1. All information, images and other assets displayed and made available for download on the lightcolourvision.org website are copyright. This means there are limitations on how they can be used.
  2. All information, images and other assets displayed or made available for download are solely and exclusively to be used for personal, educational and non-profit purposes.
  3. When you find the resources you need, then part of the download process involves you (the user) ticking a box to let us (at lightcolourvision.org) know we both agree on how the material can be used.
  4. Please contact [email protected] before considering any use not covered by the terms of the agreement above.

The copyright to all information, images and all other assets (unless otherwise stated) belongs to:

The Trustees. MediaStudies Trust
111 Lynbrooke Avenue
Blockhouse Bay
Auckland 0600
New Zealand
[email protected]

We love feedback

Your name and email address will be used solely to provide you with information you have specifically requested. See our privacy policy at https://lightcolourvision.org/privacy/.

We welcome your feedback 🙂









    Note: The feedback form records the URL of the current page


    Thank you so much for your time and effort

    PREVIOUS DIAGRAM
    NEXT DIAGRAM

    Related products