Path of a Red Ray Through a Raindrop

Path of a Red Ray Through a Raindrop

£0.00

This is one of a set of almost 40 diagrams exploring Rainbows.

Each diagram appears on a separate page and is supported by a full explanation.

  • Follow the links embedded in the text for definitions of all the key terms.
  • For quick reference don’t miss the summaries of key terms further down each page.
SKU: N/A Categories: , Tags: , ,

Description

Path of a Red Ray Through a Raindrop

TRY SOME QUICK QUESTIONS AND ANSWERS TO GET STARTED
What angle does a primary rainbow appear at from its centre?
The red band of colour on a primary rainbow appears at an angular distance of 42.4 degrees from the centre of the bow.
Does the colour of a ray of light change as it travels through different transparent media?
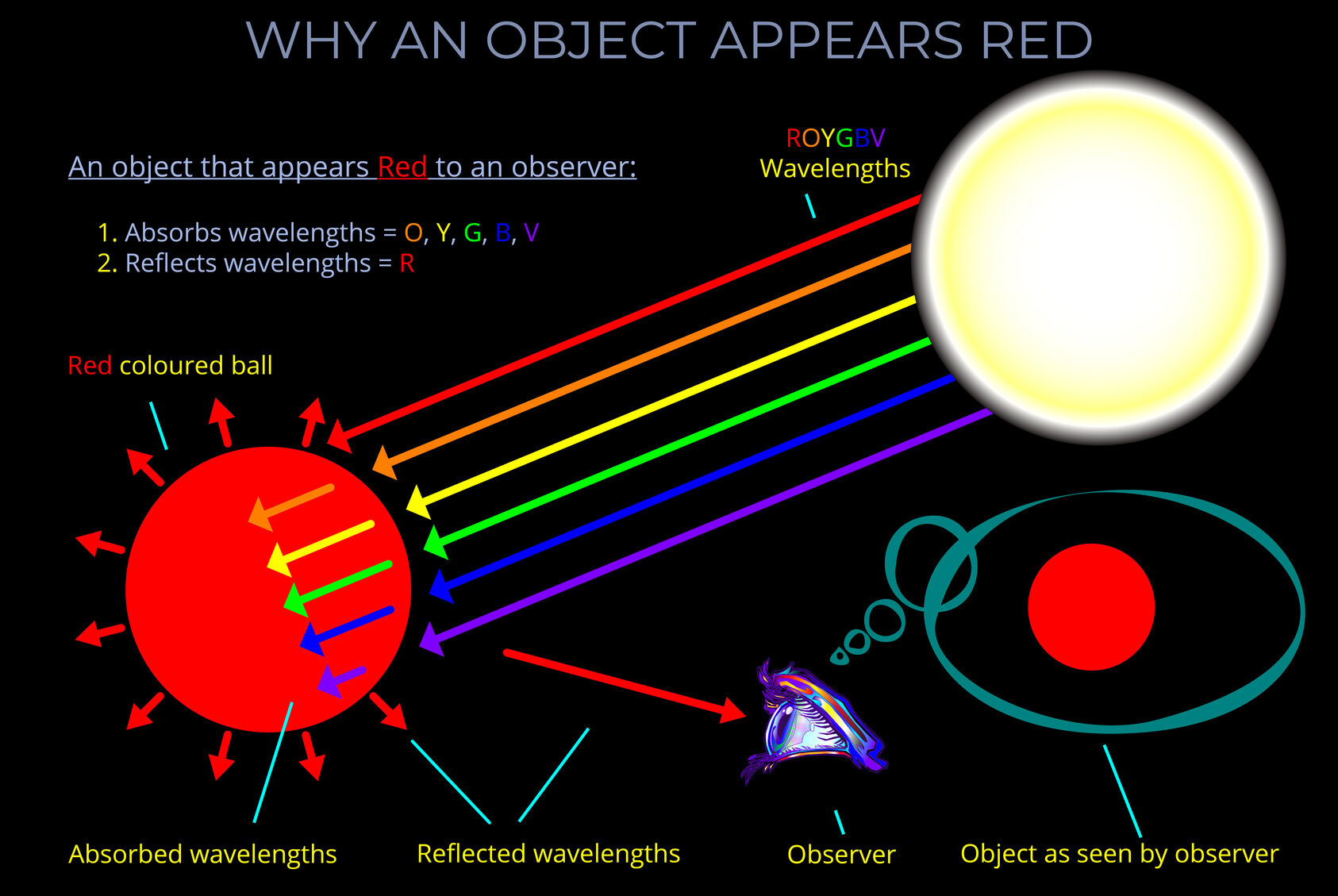
No! The colour of a ray of light remains the same as it travels through different transparent media because whilst its speed and wavelength change its frequency is not affected.
What causes dispersion of sunlight as it passes through a raindrop?
It is the small difference in the refractive index of different wavelengths of incident light that causes dispersion and separation of white light into rainbow colours.
What does angular distance refer to when an observer sees a rainbow?
Angular distance is the angle between the rainbow axis and the direction in which an observer must look to see the coloured arcs of a rainbow.
Does light travel faster in air than in raindrops?
Yes! Light travels faster in air than in water.

About the diagram

Overview of raindrops

Error: View 00a7deb7ro may not exist
Overview of raindrop geometry
Error: View 057ec7dovc may not exist
About the diagram
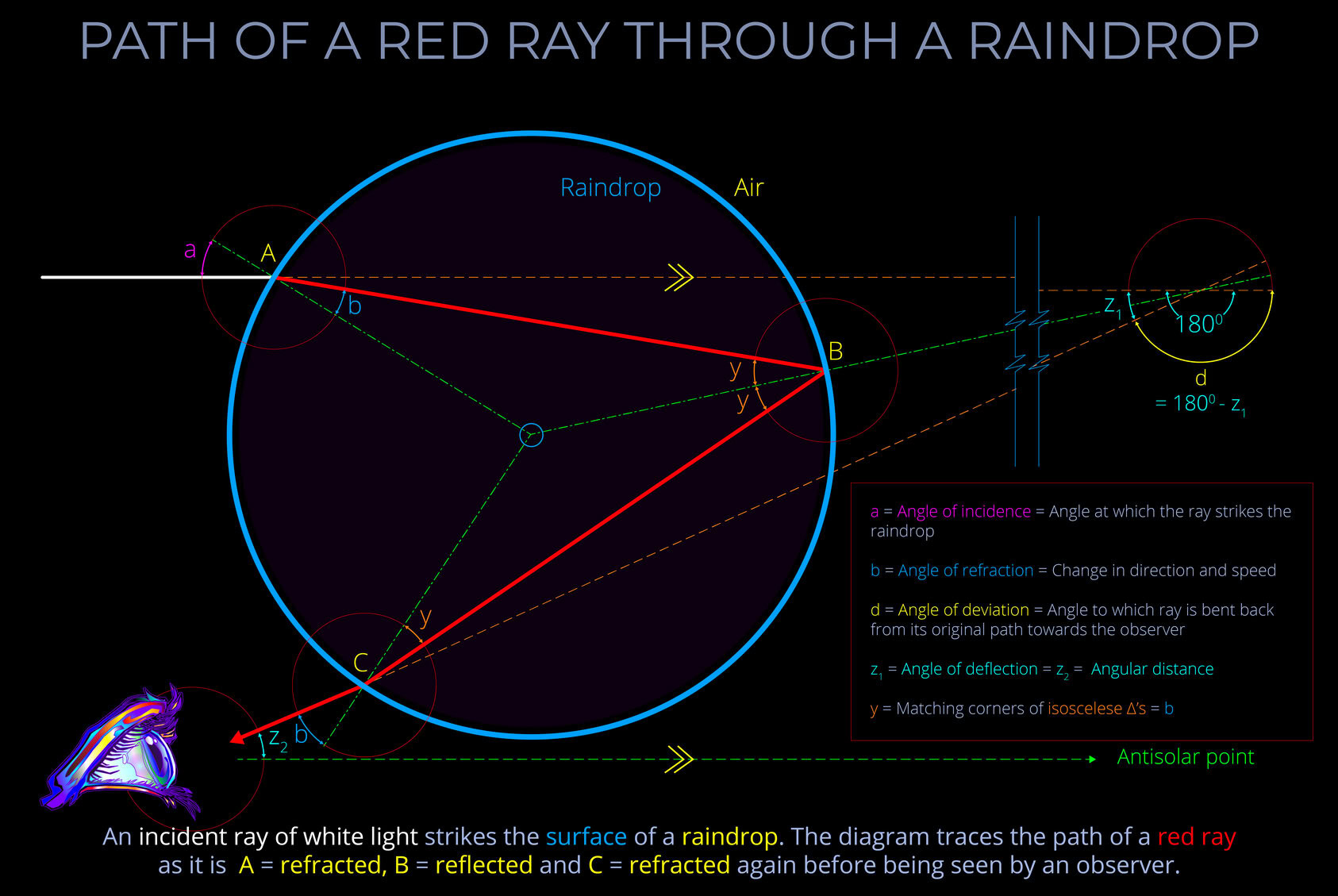
  • In this diagram, an incident ray of white light strikes the surface of a raindrop. The diagram traces the path of a red ray as it is refracted, reflected and refracted again before being seen by an observer.
  • The points at which the ray strikes the raindrop are marked as follows:
    • A = Initial point of impact of the incident ray
    • B = Point at which ray reflects off the interior of the droplet
    • C = Point at which the ray is refracted for a second time and exits the droplet towards the observer
  • The key explains the angles marked on the diagram as follows:
    • a = Angle of incidence = Angle at which the ray strikes the raindrop
    • b = Angle of refraction = Change in direction and speed
    • d = Angle of deviation = Angle to which ray is bent back from its original path towards the observer
    • z1 = Angle of deflection = z2 = Angular distance
    • y = Matching corners of isosceles Δ’s = b
Understanding the diagram
  • This page introduces a topic that is dealt with in more detail later in this series.
  • Visitors who want to develop a comprehensive understanding of the role of individual raindrops in the appearance of rainbows will find that Section 7 of Rainbows: In detail provides a thorough introduction.

Some key terms

No posts found.

Diagrams are free to download

Related products